


《频率与概率》概率PPT课件
第一部分内容:内容标准
1.结合实例,会用频率估计概率.
2.理解频率与概率的区别与联系.
3.能用概率的意义解释生活中的事例.
... ... ...
频率与概率PPT,第二部分内容:课前 • 自主探究
[教材提炼]
知识点 频率的稳定性
预习教材,思考问题
我们知道,事件的概率越大,意味着事件发生的可能性越大,在重复试验中,相应的频率一般也越大;事件的概率越小,则事件发生的可能性越小,在重复试验中,相应的频率一般也越小.在初中,我们利用频率与概率的这种关系,通过大量重复试验,用频率去估计概率.那么,在重复试验中,频率的大小是否就决定了概率的大小呢?频率与概率之间到底是一种怎样的关系呢?
[提示] 大量试验表明,在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性.一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A).
[自主检测]
1.某人将一枚硬币连续抛掷了10次,正面朝上的情形出现了6次,则( )
A.正面朝上的概率为0.6
B.正面朝上的频率为0.6
C.正面朝上的频率为6
D.正面朝上的频率接近于0.6
2.下列说法正确的是( )
A.某厂一批产品的次品率为5%,则任意抽取其中20件产品一定会发现一件次品
B.气象部门预报明天下雨的概率是90%,说明明天该地区90%的地方要下雨,其余10%的地方不会下雨
C.某医院治疗一种疾病的治愈率为10%,那么前9个病人都没有治愈,第10个人就一定能治愈
D.掷一枚均匀硬币,连续出现5次正面向上,第六次出现反面向上的概率与正面向上的概率仍然都为50%
3.在一篇英文短文中,共使用了6 000个英文字母(含重复使用),其中字母“e”共使用了900次,则字母“e”在这篇短文中的使用的频率为________.\
4.某人进行打靶练习,共射击10次,其中有2次击中10环,有3次击中9环,有4次击中8环,有1次未中靶.
(1)求此人中靶的概率;
(2)若此人射击1次,则中靶的概率约为多大?击中10环的概率约为多大?
... ... ...
频率与概率PPT,第三部分内容:课堂 • 互动探究
探究一 频率与概率的关系
[例1] 下列说法中正确的有( )
①任何事件的概率总是在[0,1]之间;
②概率是随机的,在试验前不能确定;
③频率是客观存在的,与试验次数无关;
④频率是概率的近似值,概率是频率的稳定值.
A.①④ B.②③
C.①③④ D.①②③④
[解析] 频率是不能脱离试验次数的实验值,而概率是具有确定性的不依赖于试验次数的理论值,故②③不正确.①④显然正确.
方法提升
频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率.频率本身是随机变量,当n很大时,频率总是在一个稳定值附近摆动,这个稳定值就是概率.
探究二 用频率估计概率
[例2] 某射击队统计了平日训练中两名运动员击中10环的次数,如下表:
(1)分别计算出甲、乙两名运动员击中10环的频率;
(2)根据(1)中的数据预测两名运动员在奥运会上击中10环的概率.
方法提升
1.随机事件在一次试验中是否发生虽然不能事先确定,但是在大量重复试验的情况下,它的发生呈现出一定的规律性,可以用事件发生的频率去“测量”,因此可以通过计算事件发生的频率去估算概率.
2.此类题目的解题方法是:先利用频率的计算公式依次计算出各个频率值,然后根据概率的定义确定频率的稳定值即为概率.
探究三 游戏的公平性
[例3] 某校高二年级(1)(2)班准备联合举行晚会,组织者欲使晚会气氛热烈、有趣,策划整场晚会以转盘游戏的方式进行,每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.(1)班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时(1)班代表获胜,否则(2)班代表获胜.该方案对双方是否公平?为什么?
... ... ...
频率与概率PPT,第四部分内容:课后 • 素养培优
概率统计含义的应用
数据分析、逻辑推理、数学运算
频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率,频率本身是随机变量,当n很大时,频率总是在一个稳定值附近左右摆动,这个稳定值就是概率.解此类题目的步骤是:先利用频率的计算公式依次计算出各个频率值,然后根据概率的定义确定频率的稳定值即为概率.
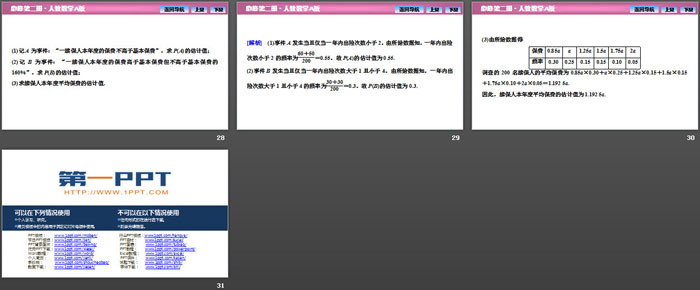
[典例] 某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 0 1 2 3 4 ≥5
保费 0.85a a 1.25a 1.5a 1.75a 2a
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 0 1 2 3 4 ≥5
频数 60 50 30 30 20 10
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
... ... ...
关键词:人教版高中数学必修二PPT课件免费下载,频率与概率PPT下载,概率PPT下载,.PPT格式;











